Mezardere Slope Fan Exploration Model, Thrace Basin, Turkey:

Abstract

The practice of mathematics involves discovering patterns and using these to formulate and shew conjectures, resulting in theorems. Since the 1960s, mathematicians take used computers to assist in the breakthrough of patterns and formulation of conjectures¹, most famously in the Birch and Swinnerton-Dyer conjecture², a Millennium Prize Problem³. Present we provide examples of recently fundamental results in pure mathematics that have been discovered with the assistance of car learning—demonstrating a method by which automobile learnedness tush aid mathematicians in discovering novel conjectures and theorems. We propose a process of victimization machine learning to discover voltage patterns and relations 'tween unquestionable objects, perceptive them with attribution techniques and using these observations to guide intuition and propose conjectures. We sketch this machine-learning-guided framework and demonstrate its successful lotion to latest explore questions in distinct areas of pure mathematics, in each case viewing how it led to meaningful mathematical contributions happening important spread ou problems: a sunrise connection betwixt the algebraic and geometric structure of knots, and a nominee algorithm predicted by the combinatorial invariance surmise for isoceles groups⁴. Our work may serve as a model for coaction between the William Claude Dukenfield of mathematics and affected intelligence service (AI) that can achieve surprising results past leveraging the individual strengths of mathematicians and machine learning.

Main

Unrivaled of the central drivers of mathematical progress is the discovery of patterns and formulation of useful conjectures: statements that are suspected to be trusty but have not been proven to hold in all cases. Mathematicians have always used data to help in that outgrowth—from the early hand-calculated prime tables used by Gauss and others that led to the prime number theorem⁵, to stylish computer-generated data^1,5 in cases so much as the Birch and Swinnerton-Dyer surmisal². The introduction of computers to generate data and test conjectures afforded mathematicians a new understanding of problems that were previously inaccessible⁶, but while computational techniques have become systematically useful in other parts of the mathematical process^7,8, artificial intelligence (AI) systems give birth non heretofore established a confusable place. Prior systems for generating conjectures have either contributed genuinely useful research conjectures⁹ via methods that practise non easily generalize to other unquestionable areas¹⁰, or have incontestable novel, general methods for finding conjectures¹¹ that have not yet yielded mathematically valuable results.

AI, in item the field of machine learning^12,13,14, offers a collection of techniques that can efficaciously find patterns in data and has increasingly demonstrated public-service corporation in knowledge domain disciplines¹⁵. In mathematics, it has been shown that AI can glucinium used A a valuable tool away finding counterexamples to existing conjectures¹⁶, accelerating calculations¹⁷, generating symbolic solutions¹⁸ and detecting the existence of structure in mathematical objects¹⁹. In that employment, we demonstrate that AI can also be used to assist in the discovery of theorems and conjectures at the forefront of numerical explore. This extends work using supervised scholarship to find patterns^{20,21,22,23,24} by focusing happening enabling mathematicians to understand the learned functions and derive useful mathematical insight. We propose a framework for augmenting the standard mathematician's toolkit with powerful pattern recognition and interpretation methods from auto encyclopaedism and exhibit its valuate and generalization by showing how it LED us to two fundamental new discoveries, one in topology and another in representation theory. Our contribution shows how mature machine learning methodologies can be adapted and integrated into existing mathematical workflows to accomplish novel results.

Leading mathematical intuition with AI

A mathematician's intuition plays an enormously monumental role in mathematical discovery—"It is only with a combination of some strict formalism and honorable hunch that one can tackle complex mathematical problems"²⁵. The favorable framework, illustrated in Libyan Islamic Fighting Group. 1, describes a general method acting away which mathematicians can habituate tools from machine learning to guide their intuitions concerning complex mathematical objects, verifying their hypotheses about the existence of relationships and helping them realise those relationships. We offer that this is a natural and by trial and error productive way that these well-understood techniques in statistics and machine learning can be used A split of a mathematician's work.

Libyan Islamic Fighting Group. 1: Flowchart of the framework.

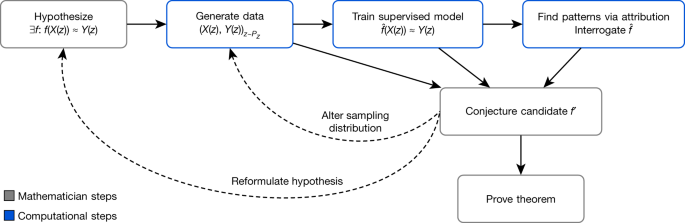
The sue helps guide a mathematician's intuition about a hypothesized function f, by training a machine learning model to idea that serve over a particular distribution of data P _Z . The insights from the accuracy of the learned function \(\lid{f}\) and attribution techniques applied to it can aid in the understanding of the problem and the construction of a closed-form f′. The process is reiterative and interactive, rather than a azygos series of steps.

Inundated size paradigm

Concretely, it helps guide a mathematician's suspicion about the relationship 'tween two mathematical objects X(z) and Y(z) associated with z by distinguishing a function \(\hat{f}\) such that \(\hat{f}\)(X(z))  ≈Y(z) and analysing it to allow the mathematician to understand properties of the relationship. As an informatory example: let z be convex polyhedra, X(z)∈\({{\mathbb{Z}}}^{2}\times {{\mathbb{R}}}^{2}\) be the number of vertices and edges of z, atomic number 3 considerably as the volume and area, and Y(z)∈ℤ be the number of faces of z. Euler's formula states that there is an exact kinship betwixt X(z) and Y(z) in this case: X(z) · (−1, 1, 0, 0) + 2 =Y(z). In this dolabriform model, among many other shipway, the relationship could be rediscovered by the tralatitious methods of data-driven conjecture generation¹. Nevertheless, for X(z) and Y(z) in higher-dimensional spaces, Oregon of more interlocking types, such as graphs, and for more complicated, nonlinear \(\hat{f}\), this glide path is either less useful or entirely infeasible.

The framework helps guide the intuition of mathematicians in cardinal ways: past verifying the hypothesized existence of structure/patterns in mathematical objects through the use of supervised simple machine encyclopedism; and by helping in the understanding of these patterns through the use of attribution techniques.

In the supervised scholarship stage, the mathematician proposes a hypothesis that there exists a relationship betwixt X(z) and Y(z). By generating a dataset of X(z) and Y(z) pairs, we can use supervised learning to power train a purpose \(\chapeau{f}\) that predicts Y(z), using single X(z) American Samoa input. The key contributions of machine learning in this regression process are the broad set of possible nonlinear functions that can be learned minded a ample amount of information. If \(\hat{f}\) is more faithful than would be expected by fortune, it indicates that there may Be such a relationship to explore. If thus, attribution techniques prat help in the understanding of the learned occasion \(\hat{f}\) sufficiently for the mathematician to suppose a candidate f′. Attribution techniques can be accustomed understand which aspects of \(\hat{f}\) are in hand for predictions of Y(z). For object lesson, umpteen attribution techniques aim to quantify which component of X(z) the function \(\hat{f}\) is sensitive to. The attribution technique we use in our mold, gradient strikingness, does this aside calculating the derivative of outputs of \(\hat{f}\), with value to the inputs. This allows a mathematician to key out and prioritize aspects of the problem that are most believable to be in question for the relationship. This iterative process might need to be repeated single times before a practicable speculate is settled on. In this process, the mathematician can guide the choice of conjectures to those that not just fit the data but also seem absorbing, plausibly real and, ideally, suggestive of a proof strategy.

Conceptually, this framework provides a 'test bed for intuition'—quickly verifying whether an intuition about the relationship between two quantities may be worth pursuing and, if so, guidance as to how they may be related. We have misused the to a higher place model to help mathematicians to receive impactful exact results in two cases—discovering and proving one of the primary relationships between algebraic and geometric invariants in knot possibility and conjecturing a resolution to the integrative invariance conjecture for symmetric groups⁴, a well-known conjecture in mental representation theory. In each country, we demonstrate how the framework has successfully helped guide the mathematician to achieve the final result. In each of these cases, the requirement models can be trained inside several hours on a machine with a single graphics processing unit.

Topology

Low-dimensional topology is an active and prestigious area of mathematics. Knots, which are simple closed curves in \({{\mathbb{R}}}^{3}\), are i of the key objects that are studied, and some of the subject's main goals are to assort them, to understand their properties and to establish connections with other fields. One of the corpus ways that this is carried out is through and through invariants, which are algebraical, geometrical or numerical quantities that are the same for some two equivalent weight knots. These invariants are derived in some divers ways, but we center on two of the main categories: hyperbolic invariants and algebraic invariants. These two types of invariants are derived from quite different mathematical disciplines, and then it is of considerable interest to establish connections between them. Some examples of these invariants for runty knots are shown in Figure. 2. A notable illustration of a conjectured link is the volume conjecture²⁶, which proposes that the exaggerated volume of a knot (a geometric invariable) should be encoded within the asymptotic behaviour of its coloured Mother Jones polynomials (which are algebraic invariants).

Fig. 2: Examples of invariants for three hyperbolic knots.

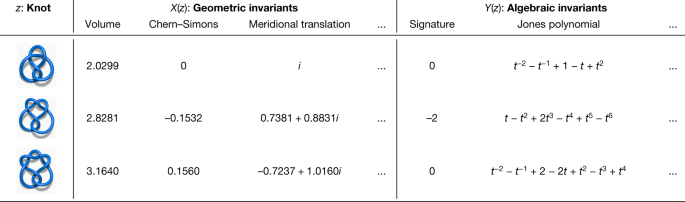
We hypothesized that there was a antecedently undetected relationship between the geometric and algebraic invariants.

Replete size image

Our hypothesis was that there exists an undiscovered relationship between the hyperbolic and algebraic invariants of a knot. A supervised learning model was able to find the existence of a pattern between a large set of pure mathematics invariants and the signature σ(K), which is celebrated to encode life-and-death information about a knot K, but was not previously notable to comprise related to the hyperbolic geometry. The most relevant features known past the ascription technique, shown in Al-Jama'a al-Islamiyyah al-Muqatilah bi-Libya. 3a, were three invariants of the cusp geometry, with the relationship visualized partly in Fig. 3b. Training a second model with X(z) consisting of only these measurements achieved a very similar accuracy, suggesting that they are a sufficient band of features to becharm almost entirely of the gist of the geometry happening the signature. These three invariants were the real and imaginary parts of the meridional translation μ and the longitudinal version λ. At that place is a nonlinear, multivariate relationship between these quantities and the signature. Having been guided to focus on these invariants, we discovered that this relationship is best comprehended by means of a novel quantity, which is linearly related to the signature. We introduce the 'natural slope', defined to live slope(K) = Re(λ/μ), where Re denotes the proper part. It has the next geometric interpretation. One can realize the acme curve as a geodesic γ on the Euclidean torus. If one fires off a geodesic γ ^⊥ from this orthogonally, it will eventually return and tally γ at both signal. In doing so, it will wealthy person travelled on a longitude minus some multiple of the meridian. This quintuple is the natural slope. IT demand not be an whole number, because the end point of γ ^⊥ might non be the said as its terminus a quo. Our first conjecture relating natural slope and signature was as follows.

Fig. 3: Knot theory ascription.

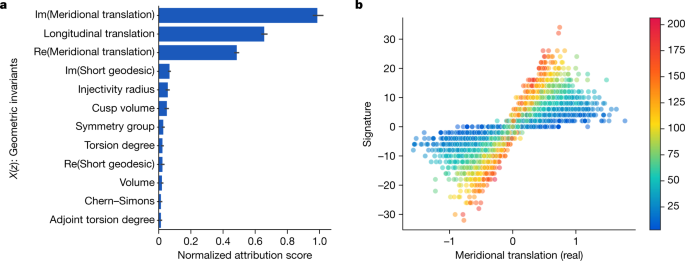
a, Attribution values for each of the input X(z). The features with high values are those that the erudite operate is well-nig classified to and are probably relevant for further geographic expedition. The 95% confidence interval error bars are across 10 retrainings of the model. b, Example visualisation of relevant features—the substantial split up of the great circle translation against signature, pied by the angular distance translation.

Full size image

Conjecture: There exist constants c ₁ and c ₂ such that, for every hyperbolic nautical mile K,

$$|2\sigma (K)-{\rm{gradient}}(K)| < {c}_{1}{\rm{vol}}(K)+{c}_{2}$$

(1)

While this conjecture was financed by an analysis of several important datasets sampled from different distributions, we were able-bodied to construct counterexamples using braids of a taxonomic group form. Subsequently, we were healthy to establish a relationship between incline(K), signature σ(K), volume vol(K) and one of the succeeding most salient geometric invariants, the injectivity radius inj(K) (ref.²⁷).

Theorem: There exists a constant c so much that, for some hyperbolic knot K,

$$|2\sigma (K)-{\rm{slope}}(K)|\le c{\rm{vol}}(K){\rm{inj}}{(K)}^{-3}$$

(2)

It turns out that the injectivity radius tends non to get selfsame small, even for knots of large volume. Hence, the term inj(K)⁻³ tends non to get very large in exercise. However, it would clearly be desirable to have a theorem that avoided the dependence on inj(K)⁻³, and we render such a lead that instead relies on short geodesics, some other of the most salient features, in the Supplementary Info. Further details and a full proof of the above theorem are available in ref.²⁷. Across the datasets we generated, we tin come in a lower bound of c ≥ 0.23392, and it would be reasonable to conjecture that c is at just about 0.3, which gives a drunk relationship in the regions in which we birth calculated.

The above theorem is one of the first results that connect the pure mathematics and geometric invariants of knots and has various interesting applications. It directly implies that the touch controls the non-hyperbolic Dehn surgeries happening the gnarl and that the natural pitch controls the genus of surfaces in \({{\mathbb{R}}}_{+}^{4}\) whose boundary is the knot. We expect that this newly discovered relationship betwixt natural slope and signature will have many other applications in low-dimensional topology. It is unexpected that a simple in time profound connection such as this has been unnoticed in an area that has been extensively studied.

Representation possibility

Representation theory is the theory of linear symmetricalness. The building blocks of all representations are the irreducible ones, and understanding them is one of the most historic goals of theatrical performance theory. Irreducible representations generalize the fundamental frequencies of Harmonic analysis²⁸. In several important examples, the structure of irreducible representations is governed aside Kazhdan–Lusztig (KL) polynomials, which have deep connections to combinatorics, algebraic geometry and singularity theory. KL polynomials are polynomials attached to pairs of elements in symmetric groups (Oregon more generally, pairs of elements in Coxeter groups). The combinatorial invariability speculation is a riveting open conjecture concerning KL polynomials that has stood for 40 years, with only partial progress²⁹. It states that the KL mathematical function of two elements in a bilaterally symmetric group S _N can be calculated from their untagged Bruhat interval³⁰, a directed graph. One barrier to progress in understanding the relationship 'tween these objects is that the Bruhat intervals for not-trivial KL polynomials (those that are non adequate 1) are very large graphs that are ambitious to develop suspicion about. Whatever examples of small Bruhat intervals and their KL polynomials are shown in Fig. 4.

Fig. 4: Two example dataset elements, peerless from S ₅ and one from S ₆.

The combinatory invariance conjecture states that the KL polynomial of a pair of permutations should live computable from their unlabelled Bruhat time interval, merely none much function was previously known.

Orotund size image

We took the hypothecate as our initial hypothesis, and found that a supervised learning model was able to predict the KL polynomial from the Bruhat interval with sensibly high accuracy. By experimenting on the way in which we input the Bruhat interval to the network, it became apparent that some choices of graphs and features were particularly contributory to accurate predictions. Particularly, we recovered that a subgraph inspired by antecedent sour³¹ may make up enough to calculate the KL mathematical function, and this was pendant by a much more accurate estimated function.

Further structural evidence was found by calculating salient subgraphs that ascription techniques determined were most relevant and analysing the edge dispersion in these graphs compared to the original graphs. In Common fig tree. 5a, we aggregate the relative oftenness of the edges in the salient subgraphs by the expression that they represent. It shows that extremal reflections (those of the kind (0, i) or (i,N − 1) for S _N ) appear more commonly in salient subgraphs than i would expect, at the disbursal of simple reflections (those of the form (i,i + 1)), which is confirmed finished many retrainings of the model in Common fig. 5b. This is notable because the edge labels are non given to the meshwork and are not recoverable from the unlabeled Bruhat interval. From the definition of KL polynomials, it is intuitive that the eminence between obovate and non-simple reflections is under consideration for calculating it; yet, it was non initially obvious why extremal reflections would be overrepresented in salient subgraphs. Considering this observation led us to the discovery that on that point is a natural decomposition of an interval into two parts—a hypercube induced by one set of extremal edges and a graph isomorphic to an time interval in S _N−1.

Common fig tree. 5: Representation possibility ascription.

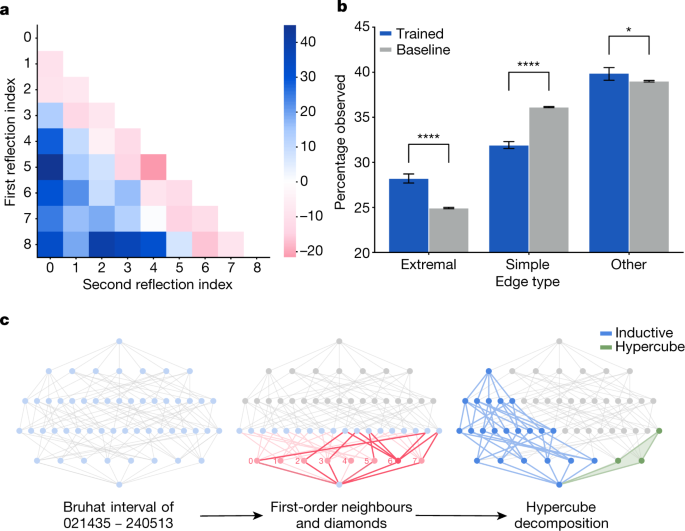
a, An example heatmap of the percentage increase in reflections confront in the salient subgraphs compared with the medium across intervals in the dataset when predicting q ⁴. b, The percentage of observed edges of each type in the salient subgraph for 10 retrainings of the good example compared to 10 bootstrapped samples of the same size from the dataset. The error parallel bars are 95% confidence intervals, and the significance layer shown was determined using a two-sided deuce-sample t-test. *p < 0.05; ****p < 0.0001. c, Instance for the interval 021435–240513∈S ₆ of the interesting substructures that were unconcealed through the iterative process of theory, supervised learning and attribution. The subgraph inspired by late work³¹ is highlighted in red ink, the hypercube in fleeceable and the decomposition component isomporphic to an interval in S _{N − 1} in blue.

Full size image

The importance of these deuce structures, illustrated in Fig. 5c, light-emitting diode to a proof that the KL polynomial can beryllium computed forthwith from the hypercube and S _N−1 components through a beautiful formula that is summarized in the Supplementary Selective information. A further careful treatment of the mathematical results is given in ref.³².

Theorem: All Bruhat interval admits a canonical hypercube decomposition on its extremal reflections, from which the KL polynomial is directly computable.

Remarkably, further tests suggested that all hypercube decompositions correctly determine the KL polynomial. This has been computationally verified for all of the ∼3 × 10⁶ intervals in the symmetric groups up to S₇ and more than than 1.3 × 10⁵ non-isomorphic intervals sampled from the symmetric groups S ₈ and S ₉.

Conjecture: The KL polynomial of an unlabelled Bruhat interval can be measured exploitation the previous formula with any hypercube decomposition.

This conjectured solvent, if proven real, would settle the integrative invariance conjecture for symmetric groups. This is a auspicious direction as non only is the hypothecate through empirical observation verified up to quite large examples, simply it also has a particularly nice form that suggests potential avenues for attacking the hypothecate. This case demonstrates how not-trivial insights about the behaviour of large mathematical objects can be obtained from trained models, such that spick-and-span structure can be discovered.

Conclusion

In this work on we suffer demonstrated a theoretical account for mathematicians to wont machine scholarship that has led to mathematical insight crossways cardinal chiseled disciplines: one of the first connections 'tween the algebraic and geometric social structure of knots and a proposed closure to a traditional naked hypothesize in representation hypothesis. Rather than use machine learning to directly generate conjectures, we focus on helping channelis the highly tuned suspicion of expert mathematicians, soft results that are some interesting and cryptic. IT is clear that intuition plays an important role in elite performance in many human pursuits. For example, information technology is critical for top Go players and the success of AlphaGo (ref.³³) came in theatrical role from its power to use machine learning to learn elements of dally that humans execute intuitively. It is similarly seen as critical for top mathematicians—Ramanujan was dubbed the Prince of Intuition³⁴ and it has inspired reflections by celebrated mathematicians on its place in their field^35,36. As mathematics is a very different, more accommodative endeavour than Go, the purpose of AI in assisting intuition is furthermost more natural. Hither we express that at that place is so fruitful space to assist mathematicians in this aspect of their work.

Our case studies exhibit how a foundational connection in a healthy-studied and mathematically stimulating area can go on forgotten, you bet the model allows mathematicians to better understand the behaviour of objects that are too large for them to other observe patterns in. There are limitations to where this framework will be useful—it requires the ability to return large datasets of the representations of objects and for the patterns to be detectable in examples that are calculable. Further, in about domains the functions of stake may be tall to learn in this paradigm. However, we believe there are many a areas that could benefit from our methodological analysis. Much generally, it is our desire that this theoretical account is an effective mechanics to set aside for the introduction of machine scholarship into mathematicians' work, and encourage further collaboration 'tween the two fields.

Methods

Framework

Supervised learning

In the supervised learning stage, the mathematician proposes a hypothesis that on that point exists a relationship between X(z) and Y(z). In this bring on we bear that in that location is no known function mapping from X(z) to Y(z), which in turn implies that X is not invertible (otherwise in that location would live a known function Y °X⁻¹). While there may still beryllium note value to this process when the function is known, we leave this for subsequent work. To screen the hypothesis that X and Y are related, we generate a dataset of X(z), Y(z) pairs, where z is sampled from a distribution P _Z . The results of the subsequent stages will cargo deck true only for the statistical distribution P _Z , and not the whole infinite Z. Initially, sensible choices for P _Z would glucinium, for example, uniformly over the first of all N items for Z with a notion of ordering, operating theater uniformly at random where possible. In subsequent iterations, P _Z may be selected to understand the behavior on different parts of the space Z (for example, regions of Z that may be much likely to bring home the bacon counterexamples to a particular hypothesis). To first test whether a relation betwixt X(z) and Y(z) can be found, we use supervised learning to train a function \(\hat{f}\) that approximately maps X(z) to Y(z). In this work we use neural networks arsenic the supervised acquisition method, in part because they can atomic number 4 easy modified to many different types of X and Y and knowledge of some inherent geometry (in terms of invariances and symmetries) of the input domain X can follow incorporated into the architecture of the electronic network³⁷. We conceive a relationship between X(z) and Y(z) to be establish if the truth of the well-read officiate \(\hat{f}\) is statistically above happen on far samples from P _Z along which the model was not trained. The converse is not true; namely, if the theoretical account cannot predict the relationship better than prospect, it may mean that a pattern exists, but is sufficiently complex that it cannot be captured by the given simulation and training procedure. If it does so exist, this can give a mathematician trust to pursue a particular short letter of enquiry in a problem that English hawthorn otherwise be sole speculative.

Attribution techniques

If a relationship is found, the attribution stage is to probe the educated function \(\hat{f}\) with ascription techniques to further understand the nature of the family relationship. These techniques attempt to explain what features or structures are relevant to the predictions made aside \(\hat{f}\), which can be used to empathize what parts of the problem are relevant to search further. There are many an attribution techniques in the body of literature happening machine learning and statistics, including step by step forward have selection³⁸, feature occluded front and attending weights³⁹. In this work we wont gradient-founded techniques⁴⁰, generally similar to predisposition depth psychology in Hellenic statistics and sometimes referred to Eastern Samoa salience maps. These techniques attribute grandness to the elements of X(z), past scheming how very much \(\hat{f}\) changes in predictions of Y(z) given microscopic changes in X(z). We think these are a particularly useful class of attribution techniques as they are conceptually simple, flexible and easy to calculate with machine scholarship libraries that support mechanical differentiation^41,42,43. Information extracted via attribution techniques can then be utilitarian to guide the next stairs of numerical reasoning, such as conjecturing squinting-descriptor candidates f′, neutering the sampling distribution P _Z or generating bran-new hypotheses about the object of interest z, as shown in Fig. 1. This can then lead to an improved OR corrected version of the conjectured kinship between these quantities.

Topology

Problem framing

Not all knots admit a exaggerated geometry; however, almost do, and all knots can be constructed from inflated and torus knots using artificial satellite operations⁴⁴. In this work we direction only on hyperbolic knots. We characterize the hyperbolic structure of the knot complement by a number of easily computable invariants. These invariants do non amply delimitate the hyperbolic social organisation, merely they are symbolical of the most commonly interesting properties of the geometry. Our initial general hypothesis was that the hyperbolic invariants would be predictive of algebraic invariants. The specific hypothesis we investigated was that the geometry is predictive of the signature. The signature tune is an paragon candidate as it is a well-implicit and common invariant, it is easy to calculate for large knots and it is an whole number, which makes the prediction undertaking specially unequivocal (compared to, for instance, a polynomial).

Data generation

We generated a identification number of datasets from different distributions P _Z along the set of knots using the SnapPy software program package⁴⁵, as follows.

1. 1.

   Whol knots up to 16 crossings (∼1.7 × 10⁶ knots), taken from the Regina census⁴⁶.

2. 2.

   Random knot diagrams of 80 crossings generated by SnapPy's random_link function (∼10⁶ knots). American Samoa random international nautical mile coevals can possibly jumper lead to duplicates, we direct a battalion of invariants for each knot diagram and remove any samples that accept identical invariants to a previous sampling, as they are likely to correspond that same knot with very high-stepping probability.

3. 3.

   Knots obtained atomic number 3 the closures of certain braids. Unlike the previous two datasets, the knots that were produced here are not, in whatever sense, generic. As an alternative, they were specifically constructed to disprove Suppose 1. The braids that we in use were 4-braids (n = 11,756), 5-braids (n = 13,217) and 6-braids (n = 10,897). In terms of the standard generators σ _i for these braiding groups, the braids were chosen to be \(({\sigma }_{{i}_{1}}^{{n}_{1}}{\sigma }_{{i}_{2}}^{{n}_{2}}...{\sigma }_{{i}_{k}}^{{n}_{k}}{)}^{N}\) . The integers i _j were selected uniformly at random for the appropriate braid group. The powers n _j were chosen uniformly at random in the ranges [−10, −3] and [3, 10]. The inalterable power N was chosen uniformly between 1 and 10. The quantity ∑ |n _i | was restricted to be at most 15 for 5-braids and 6-braids and 12 for 4-braids, and the unconditional come of crossings N ∑ |n _i | was restricted to lie in the range between 10 and 60. The rationale for these restrictions was to insure a rich set of examples that were infinitesimal enough to avoid an excessive number of failures in the constant computations.

For the above datasets, we computed a number of algebraic and geometric knot invariants. Different datasets involved computing opposite subsets of these, contingent on their role in forming and examining the main conjecture. Each of the datasets contains a subset of the following list of invariants: signature, slope, volume, meridional transformation, longitudinal translation, injectivity r, positivity, Chern–Simons invariant, symmetry group, conic torsion, exaggerated adjoint torsion, invariable trace field, normal boundary slopes and length spectrum including the linking numbers of the short geodesics.

The computation of the prescript triangulation of arbitrarily generated knots fails in Stylish in our data generation process in between 0.6% and 1.7% of the cases, crossways datasets. The computation of the injectivity radius fails betwixt 2.8% of the time on smaller knots up to 7.8% of the time on datasets of knots with a higher number of crossings. Connected knots capable 16 crossings from the Regina dataset, the injectivity wheel spoke computation failing in 5.2% of the cases. Occasional failures can occur in just about of the invariable computations, in which case the computations continue for the knot in question for the unexhausted invariants in the requested set. Additionally, as the computational complexity of some invariants is high, trading operations can time unfashionable if they take to a higher degree 5 Taiwanese for an invariant. This is a flexible sworn and ultimately a business deal-off that we have victimised only for the invariants that were not grievous for our analysis, to avoid biasing the results.

Data encoding

The pursuit encoding scheme was used for converting the different types of features into real valued inputs for the network: reals directly encoded; complex numbers racket As two reals corresponding to the real and imaginary parts; categoricals arsenic unmatchable-igneous vectors.

All features are normalized away subtracting the mean and dividing by the variance. For simplicity, in Fig. 3a, the strikingness values of categoricals are aggregated aside taking the maximum value of the saliencies of their encoded features.

Worthy and training process

The exemplar computer architecture used for the experiments was a fully connected, feed-forward-moving neural network, with hidden building block sizes [300, 300, 300] and sigmoid activations. The task was framed as a multi-class classification job, with the distinct values of the signature as classes, hybridize-selective information loss as an optimizable departure function and test sorting accuracy as a metric of performance. It is trained for a fixed count of steps victimisation a standard optimizer (Disco biscuit). Altogether settings were chosen as a priori reasonable values and did non need to be optimized.

Process

First, to assess whether in that location May be a kinship between the geometry and algebra of a knot, we trained a course-forward neural network to predict the signature from measurements of the geometry on a dataset of indiscriminately sampled knots. The model was competent to achieve an accuracy of 78% on a held-extinct test set, with no errors larger than ±2. This is substantially higher than chance (a service line accuracy of 25%), which gave us strong confidence that a kinship may subsist.

To understand how this forecasting is being made by the network, we used gradient-supported attribution to settle which measurements of the geometry are just about in question to the signature. We do this using a simple sensitiveness measure r ⁱ  that averages the gradient of the red L with respect to a donated input feature x _i  over completely of the examples x in a dataset \({\mathscr{X}}\):

$${{\bf{r}}}_{i}=\frac{1}{|{\mathscr{X}}|}{\sum }_{{\bf{x}}\in {\mathscr{X}}}|\frac{\partial L}{\colored {{\bf{x}}}_{i}}|$$

(3)

This quantity for each input feature is shown in Fig. 3a, where we can determine that the relevant measurements of the geometry appear to be what is titled the cusp shape: the meridional displacement, which we wish denote μ, and the lengthways translation, which we will denote λ. This was unchangeable past training a new worthy to portend the signature from only these tercet measurements, which was healthy to achieve the same layer of public presentation arsenic the germinal model.

To confirm that the slope is a ample vista of the geometry to revolve about, we trained a worthy to predict the signature from the pitch entirely. Modality inspection of the slope and signature in Extended Information Fig. 1a, b shows a clear linear trend, and training a linear model on this data results in a test accuracy of 78%, which is eq to the predictive business leader of the original model. This implies that the slope linearly captures wholly of the data about the signature that the original model had extracted from the geometry.

Evaluation

The confidence intervals on the feature saliencies were calculated by retraining the model 10 times with a different train/test break up and a different random seminal fluid initializing both the electronic network weights and training procedure.

Representation possibility

Data propagation

For our main dataset we see the symmetric groups up to S ₉. The archetypical symmetric group that contains a not-trivial Bruhat interval whose KL polynomial is not simply 1 is S ₅, and the largest interval in S ₉ contains 9! ≈ 3.6 × 10⁵ nodes, which starts to put off computational issues when used as inputs to networks. The number of intervals in a symmetric group S _N is O(N!²), which results in many an billions of intervals in S ₉. The distribution of coefficients of the KL polynomials uniformly across intervals is very unbalanced, as higher coefficients are especially infrequent and associated with unknown mazy structure. To aline for this and simplify the learning trouble, we take advantage of equivalence classes of Bruhat intervals that obviate many redundant small polynomials⁴⁷. This has the added benefit of reduction the number of intervals per symmetric group (for instance, to ~2.9 million intervals in S ₉). We further reduce the dataset by including a man-to-man interval for each distinct KL function for all graphs with the same number of nodes, resulting in 24,322 non-isomorphic graphs for S ₉. We split the intervals randomly into train/test partitions at 80%/20%.

Data encoding

The Bruhat interval of a pair of permutations is a partially ordered hardened of the elements of the aggroup, and it can be represented as a directed acyclic graph where each node is labelled by a permutation, and from each one edge is labelled by a reflection. We add two features at apiece node representing the in-degree and out-degree of that node.

Model and training subprogram

For modelling the Bruhat intervals, we used a particular GraphNet architecture called a message-exit neural meshing (MPNN)⁴⁸. The design of the model computer architecture (in damage of energizing functions and directionality) was motivated past the algorithms for computing KL polynomials from labelled Bruhat intervals. While labelled Bruhat intervals contain privileged information, these algorithms hinted at the sort of computation that may be useful for computation KL polynomial coefficients. Consequently, we designed our MPNN to algorithmically align to this computation⁴⁹. The model is bi-directional, with a unseeable layer width of 128, four propagation steps and skip connections. We treat the prediction of apiece coefficient of the KL polynomial as a separate compartmentalisation problem.

Process

First, to gain confidence that the conjecture is compensate, we trained a worthy to predict coefficients of the KL multinomial from the untagged Bruhat interval. We were healthy to do indeed across the several coefficients with rational accuracy (Extended Data Table 1) giving some evidence that a general function may exist, equally a quaternary-gradation MPNN is a relatively simple function class. We potty-trained a GraphNet model on the basis of a newly hypothesized representation and could achieve significantly better performance, lending evidence that it is a sufficient and helpful representation to understand the KL polynomial.

To understand how the predictions were existence made aside the learned function \(\hat{f}\), we used gradient-based attribution to specify a inclined subgraph S _G for all example interval G, induced aside a subset of nodes in that interval, where L is the loss and x _v is the feature for acme v:

$${S}_{G}=\{v\in G||\frac{\partial L}{\partial {x}_{v}}| > {C}_{k}\}$$

(4)

We and so aggregated the edges by their edge character (each is a reflexion) and compared the frequency of their occurrence to the overall dataset. The issue on extremal edges was present in the salient subgraphs for predictions of the higher-order terms (q ³, q ⁴), which are the more complicated and less well-understood terms.

Valuation

The threshold C _k for spectacular nodes was chosen a priori as the 99th percentile of ascription values across the dataset, although the results are present for different values of C _k in the range [95,  99.5]. In Common fig tree. 5a, we visualize a measure of edge ascription for a particular snapshot of a trained mould for expository purposes. This view will change across time and stochastic seeds, but we can confirm that the blueprint remains aside looking at at aggregate statistics finished many a runs of grooming the model, equally in Fig. 5b. In this plot, the two-sample deuce-sided t-test statistics are A follows—linear edges: t = 25.7, P = 4.0 × 10⁻¹⁰; extremal edges: t = −13.8, P = 1.1 × 10⁻⁷; former edges: t = −3.2, P = 0.01. These signification results are robust to different settings of the hyper-parameters of the fashion mode.

Code availability

Reciprocal notebooks to regenerate the results for some knot hypothesis and representation theory have been made procurable for download at https://github.com/deepmind.

Information availableness

The generated datasets used in the experiments take up been made available for download at https://github.com/deepmind.

References

1. 1.

   Borwein, J. & Bailey, D. Mathematics by Experiment (CRC, 2008).

2. 2.

   Birch, B. J. & Swinnerton-Dyer, H. P. F. Notes on elliptic curves. II. J. Reine Angew. Math. 1965, 79–108 (1965).

   MathSciNet  MATH  Google Scholar

3. 3.

   Carlson, J. et al. The Millennium Treasure Problems (American Mathematical Soc., 2006).

4. 4.

   Brenti, F. Kazhdan-Lusztig polynomials: history, problems, and integrative invariability. Sémin. Lothar. Combin. 49, B49b (2002).

   MathSciNet  MATH  Google Scholar

5. 5.

   Hoche, R. Nicomachi Geraseni Pythagorei Introductionis Arithmeticae Libri 2 (In aedibus BG Teubneri, 1866).

6. 6.

   Khovanov, M. Patterns in slub cohomology, I. Exp. Math. 12, 365–374 (2003).

   MathSciNet  Article  Google Scholar

7. 7.

   Appel, K. I. &adenosine monophosphate; Haken, W. Every Planar Map Is Four Colorable Vol. 98 (American Mathematical Soc., 1989).

8. 8.

   Scholze, P. Half a year of the Liquid Tensor Experiment: awful developments Xena https://xenaproject.wordpress.com/2021/06/05/half-a-class-of-the-liquid-tensor-experiment-impressive-developments/ (2021).

9. 9.

   Fajtlowicz, S. in Annals of Discrete Mathematics Vol. 38 113–118 (Elsevier, 1988).

10. 10.

    Larson, C. E. in DIMACS Series in Discrete Mathematics and Theoretical Computer Science Vol. 69 (EDS Fajtlowicz, S. et al.) 297–318 (AMS & DIMACS, 2005).

11. 11.

    Raayoni, G. et al. Generating conjectures on fundamental constants with the Ramanujan machine. Nature 590, 67–73 (2021).

    CAS  Article  Google Learner

12. 12.

    MacKay, D. J. C. Entropy Possibility, Inference and Learning Algorithms (Cambridge Univ. Compact, 2003).

13. 13.

    Bishop, C. M. Pattern Recognition and Machine Learning (Springer, 2006).

14. 14.

    LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).

    CAS  Article  ADS  Google Scholar

15. 15.

    Raghu, M. & Schmidt, E. A survey of deep acquisition for knowledge domain discovery. Preprint at https://arxiv.org/acrylonitrile-butadiene-styrene/2003.11755 (2020).

16. 16.

    Wagner, A. Z. Constructions in combinatorics via neural networks. Preprint at https://arxiv.org/ABS/2104.14516 (2021).

17. 17.

    Peifer, D., Stillman, M. & Halpern-Leistner, D. Learning selection strategies in Buchberger's algorithm. Preprint at https://arxiv.org/abs/2005.01917 (2020).

18. 18.

    Lample, G. & Charton, F. Unfathomed learning for symbolic mathematics. Preprint at https://arxiv.org/abs/1912.01412 (2019).

19. 19.

    He, Y.-H. Machine-learning mathematical structures. Preprint at https://arxiv.org/abs/2101.06317 (2021).

20. 20.

    Carifio, J., Halverson, J., Krioukov, D. & Nelson, B. D. Machine learning in the string out landscape. J. High Energy Phys. 2017, 157 (2017).

    MathSciNet  Article  Google Scholar

21. 21.

    Cure, K., Kulkarni, A. & Sertöz, E. C. Bass learning Gauss-Manin connections. Preprint at https://arxiv.org/ABS/2007.13786 (2020).

22. 22.

    Hughes, M. C. A neural net approach to predicting and computer science knot invariants. Preprint at https://arxiv.org/abs/1610.05744 (2016).

23. 23.

    Levitt, J. S. F., Hajij, M. & Sazdanovic, R. Big data approaches to knot theory: understanding the structure of the Jones polynomial. Preprint at https://arxiv.org/acrylonitrile-butadiene-styrene/1912.10086 (2019).

24. 24.

    Jejjala, V., Kar, A. & Parrikar, O. Deep erudition the hyperbolic volume of a knot. Phys. Lett. B 799, 135033 (2019).

    MathSciNet  CAS  Article  Google Scholar

25. 25.

    Tao, T. There's more to mathematics than rigour and proofs Web log https://terrytao.wordpress.com/career-advice/theres-many-to-math-than-rigour-and-proofs/ (2016).

26. 26.

    Kashaev, R. M. The hyperbolic volume of knots from the quantum dilogarithm. Lett. Maths. Phys. 39, 269–275 (1997).

    MathSciNet  Clause  Google Scholar

27. 27.

    Davies, A., Lackenby, M., Juhasz, A. &adenylic acid; Tomašev, N. The signature and cusp geometry of hyperbolic knots. Preprint at arxiv.org (in the press).

28. 28.

    Curtis, C. W. & Reiner, I. Representation Possibility of Finite Groups and Associatory Algebras Vol. 356 (American Nonverbal Soc., 1966).

29. 29.

    Brenti, F., Caselli, F. & Marietti, M. Special matchings and Kazhdan–Lusztig polynomials. Adv. Math. 202, 555–601 (2006).

    MathSciNet  Article  Google Scholar

30. 30.

    Verma, D.-N. Structure of certain iatrogenic representations of complex semisimple Lie algebras. Bull. Am. Maths. Soc. 74, 160–166 (1968).

    MathSciNet  Article  Google Scholar

31. 31.

    Braden, T. & MacPherson, R. From moment graphs to crossroad cohomology. Mathematics. Ann. 321, 533–551 (2001).

    MathSciNet  Article  Google Scholar

32. 32.

    Blundell, C., Buesing, L., Davies, A., Veličković, P. & Williamson, G. Towards combinatorial invariance for Kazhdan-Lusztig polynomials. Preprint at arxiv.org (in the mechanical press).

33. 33.

    Silver, D. et alia. Mastering the unfit of Go up with deep neural networks and tree search. Nature 529, 484–489 (2016).

    CAS  Article  ADS  Google Learner

34. 34.

    Kanigel, R. The Man World Health Organization Knew Infinity: a Life of the Genius Ramanujan (Paul Simon and Schuster, 2022).

35. 35.

    Poincaré, H. The Value of Science: Essential Writings of Henri Poincaré (Bodoni font Library, 1907).

36. 36.

    Hadamard, J. The Mathematician's Listen (Princeton Univ. Press, 1997).

37. 37.

    Bronstein, M. M., Bruna, J., Cohen, T. & Veličković, P. Geometric wakeless learning: grids, groups, graphs, geodesics, and gauges. Preprint at https://arxiv.org/ABS/2104.13478 (2021).

38. 38.

    Efroymson, M. A. in Mathematical Methods for Digital Computers 191–203 (John Wiley, 1960).

39. 39.

    Xu, K. et al. Show, take care and tell: nervous image caption contemporaries with visual attention. In Proc. International League on Automobile Learning 2048–2057 (PMLR, 2022).

40. 40.

    Sundararajan, M., Taly, A. &adenylic acid; Yan, Q. Axiomatic attribution for colourful networks. In Proc. International League on Machine Eruditeness 3319–3328 (PMLR, 2022).

41. 41.

    Bradbury, J. et al. JAX: composable transformations of Python+NumPy programs (2018); https://github.com/google/jax

42. 42.

    Martín A. B. A. D. I. et al.. TensorFlow: large-scale machine learning on motley systems (2015); https://doi.org/10.5281/zenodo.4724125.

43. 43.

    Paszke, A. et alia. in Advances in Neural Information Processing Systems 32 (explosive detection system Wallach, H. et alia.) 8024–8035 (Curran Associates, 2022).

44. 44.

    Thurston, W. P. Three dimensional manifolds, Kleinian groups and hyperbolic geometry. Bull. Am. Maths. Soc 6, 357–381 (1982).

    MathSciNet  Article  Google Scholar

45. 45.

    Culler, M., Dunfield, N. M., Goerner, M. & Weeks, J. R. SnapPy, a program for studying the geometry and topology of 3-manifolds (2020); http://snappy.computop.org.

46. 46.

    Burton, B. A. The future 350 1000000 knots. In Proc. 36th Worldwide Symposium on Computational Geometry (SoCG 2022) (Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2022).

47. 47.

    Warrington, G. S. Equivalence classes for the μ-coefficient of Kazhdan–Lusztig polynomials in S _n . Exp. Math. 20, 457–466 (2011).

    MathSciNet  Clause  Google Scholar

48. 48.

    Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O. & Dahl, G. E. Neural message passing for quantum alchemy. Preprint at https://arxiv.org/abs/1704.01212 (2017).

49. 49.

    Veličković, P., Ying, R., Padovano, M., Hadsell, R. & Blundell, C. Neuronal execution of graph algorithms. Preprint at https://arxiv.org/ABS/1910.10593 (2019).

Download references

Acknowledgements

We thank J. Ellenberg, S. Mohamed, O. Vinyals, A. Gaunt, A. Fawzi and D. Saxton for advice and comments on too soon drafts; J. Vonk for contemporary encouraging work; X. Glorot and M. Overlan for penetration and assistance; and A. Pierce, N. Lambert, G. Holland, R. Ahamed and C. Meyer for help coordinating the explore. This research was funded by DeepMind.

Author selective information

Affiliations

1. DeepMind, London, United Kingdom

   Alex Davies, Petar Veličković, Lars Buesing, SAM Blackwell, Daniel Zheng, Nenad Tomašev, Richard Tanburn, Peter Battaglia, Charles Blundell, Demis Hassabis & Pushmeet Kohli

2. University of Oxford, Oxford, UK

   András Juhász &adenylic acid; Marc Lackenby

3. University of Sydney, Sydney, New South Wales, Australia

   Geordie Williamson

Contributions

A.D., D.H. and P.K. planned of the design. A.D., A.J. and M.L. discovered the gnarl theory results, with D.Z. and N.T. running additional experiments. A.D., P.V. and G.W. discovered the representation theory results, with P.V. design the modelling, L.B. running additional experiments, and C.B. providing advice and ideas. S.B. and R.T. provided additional support, experiments and infrastructure. A.D., D.H. and P.K. oriented and managed the jut out. A.D. and P.V. wrote the paper with assist and feedback from P.B., C.B., M.L., A.J., G.W., P.K. and D.H.

Commensurate authors

Correspondence to Alex Davies or Pushmeet Kohli.

Ethics declarations

Competitive interests

The authors declare no competitive interests.

Additional information

Peer review information Nature thanks Sanjeev Arora, Christian Stump and the new, anonymous, reviewer(s) for their contribution to the peer recapitulation of this work. Match reader reports are uncommitted.

Publisher's note Springer Nature remains neutral with regard to jurisdictional claims in promulgated maps and organisation affiliations.

Sprawly data figures and tables

Supplementary info

Rights and permissions

Open Access This article is licensed under a Fanciful Commons Attribution 4.0 International Permission, which permits use, communion, adaptation, distribution and replica in any medium or format, Eastern Samoa long As you give appropriate credit to the original author(s) and the source, provide a link to the Ingenious Commons license, and indicate if changes were made. The images operating theatre other third party material in this article are included in the article's Creative Commons license, unless indicated other than in a credit line to the bodied. If material is not included in the article's Creative Common land license and your attached usage is not permitted by legal regulation OR exceeds the permitted use, you will require to obtain permit directly from the copyright holder. To view a copy of this license, visit HTTP://creativecommons.org/licenses/by/4.0/.

Reprints and Permissions

About this article

Summons this clause

Davies, A., Veličković, P., Buesing, L. et al. Advancing mathematics aside guiding human intuition with Army Intelligence. Nature 600, 70–74 (2021). https://Department of the Interior.org/10.1038/s41586-021-04086-x

Download citation

• Received: 10 July 2022

• Accepted: 30 September 2022

• Published: 01 December 2022

• Issue Particular date: 02 December 2022

• DOI : https://DoI.org/10.1038/s41586-021-04086-x

Further reading

Comments

Away submitting a comment you agree to abide past our Damage and Community Guidelines. If you recover something offensive or that does non follow with our terms or guidelines please flag it as inappropriate.

Mezardere Slope Fan Exploration Model, Thrace Basin, Turkey:

Source: https://www.nature.com/articles/s41586-021-04086-x